GTORB Flop Sneak Preview -- 3 Street Barreling Game

As most of you know I've been working on getting GTORangeBuilder ready to solve flop scenarios. I still have a ways to go before the flop solver is ready for public release but I thought I'd share a sneak peek of a very simple solution to a 3 street version of the bluffing game that we looked at in GTO Brainteaser #8.

As it turns out we'll need to look at a smaller bet size than we did in brainteaser #8, as with three half pot bets left against a 50% nuts 50% air range the villain actually cannot profitably ever call and the hero can take the entire pot so its not a very interesting example.  Instead we'll look at a smaller bet stack size.

1. You are on the flop and the board is  AsAhKs
2. The hero has hand range of AcAd and 3c2c
3. The villain has a hand range of KcKh
4. The pot is 100 chips and stacks are 154.8 chips (exactly enough to 3-barrel 30% pot)
5. The hero can either bet 30% of the pot or shove on every street

Thus as the hero, half of our range is the pure nuts and the other half is almost pure air (we split the pot on runner runner aces).  A browseable GTORangeBuilder solution is at the bottom of the post so if the math doesn't interest you, just scroll down.  The main takeaways will come as no surprise if you understand the two street game.  Each additional street just makes it more and more difficult for the villain to get to showdown, driving his EV down.

Mathematical Solution

I'll go through the mathematical solution to this a bit quickly.  In practice it is important to check for pure strategy solutions, rather than just assuming indifference but to keep this example simple I will skip that step. 

Assume the villain plays a mixed strategy and calls some of the time on all streets except that

1. When the turn or river is an Ace he shoves because he knows the hero has air
2. When the turn or river is 3c or 2c he folds because he knows his opponent holds the nuts

We'll also assume that it is optimal for our hero to play a mixed strategy between betting and check/folding with his air on all streets, except that when an Ace comes he will check/fold because his hand is now face up.

Finally we will assume that the hero always bets the nuts.

If the hero is mixing between checking and betting air and never checks the nuts then his EV when he checks air is 0.  So his EV when he bets air must also be zero, and his EV with air on all streets must be 0 minus however much he put into the pot on prior streets.

This means that for all streets the villain needs to call to make him indifference between betting and folding so if we call c the probability that the villain calls a 30% pot bet

(1-c) * 1 - .3 * c = 0

So c = 1/1.3 = .769.

That is the villains calling frequency on all streets against a 30% pot bet.  Of course as we saw in the solution to brainteaser 8 the hero should never jam as he is then not able to compound the nuts over multiple street and maximize fold equity.

What about the hero?  To make the villain indifferent between calling and folding to a bet, on a blank river after the flop and turn when bet/call he should bet a range that is .3/1.3 nuts to air according to the mathematics of poker.  

On a blank turn what is the villains EV for calling assuming he plays his GTO on the river?  We'll split it into two cases, the case where his opponent holds air and the case where his opponent holds the nuts.  Everything is written in terms of turn pots.

He always loses the .3 pot turn bet he calls and then on blank rivers (which come 42/44) he loses another .3 of the 1.6 river pot when he calls a river bet (which he does 1/1.3).

EV[call vs nuts] = -.3 - (42/44 * .3 * 1.6 * 1 / 1.3)

Against air his opponents EV is always 0 so he wins the pot plus the .3 bet

EV[call vs air] = 1.3

Call x the percent of the hero's blank turn betting range that is the nuts.  The villain is indifferent between calling and folding when

x * EV[call vs nuts] + (1-x) * EV[call vs air] = 0

Plugging this into wolfram alpha tells us that x should be .665.

Finally we can reproduce the exact same method of indifference calculation to determine the optimal flop betting frequency.  Rewriting the call EV equations from above on the flop is easy, they are almost identical, except that when both the turn and the river come blank the villain will call a 3rd value bet 1/1.3.  The EVs below are written in terms of flop pots.

EV[call vs nuts] = -.3 - (43/45 * 1/1.3 * (.3 * 1.6  + 42/44 * .3 * 2.56 * 1/1.3))
EV[call vs air] = 1.3

EV[call vs nuts] = -.5 - (43/45 * 1/1.5 * (.5 * 2  + 42/44 * .5 * 4 * 1/1.5))
EV[call vs air] = 1.5

Resolving x * EV[call vs nuts] + (1-x) * EV[call vs air] = 0 gives us

x = .549 according to wolfram alpha.

So how often should the hero bluff his air on the flop?  Since he is always betting his nuts and his range should be .549 nuts, he should bet his air with frequency a such that 1/(1+a) = .549, or a = .821.

Then on the turn his starting range is .549 nuts and he wants to bet a range that is .665 nuts.  Thus he should bet air with a frequency that solves .549 / (.549 + a * (1-.549)) = .665 or a = .6132.

Then on the river the hero's betting range should be 1.3/1.6 = .8125 nuts so the hero should bet with his air with a frquency that solves .665 / (.665 + a * (1-.665)) = .8125 or a = 0.458

Finally what is the EV for the game?  Since the villain's EV for calling a flop bet is zero, he only gets EV when the hero checks the flop in which case he wins the whole pot since the hero always has air.

The hero checks the flop with air 1 - .821 = .179 and the hero holds air half the time so his EV will be .179 / 2 * 100 = 8.95 chips, while the hero's EV will be 91.05.

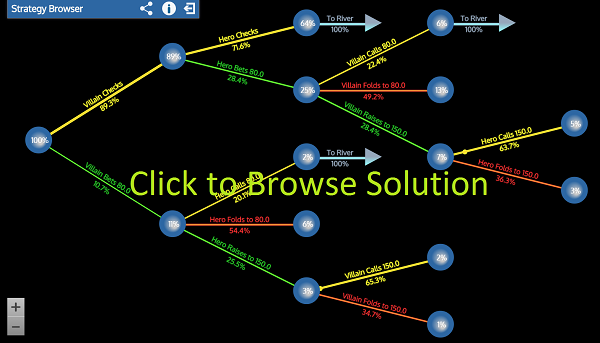
That's our mathematical solution, you can see how it matches GTORangeBuilders computational solution below.

GTORangeBuilder Computational Solution