This game turns out to have concrete testable predictions about how we should optimize our turn play in real world scenarios which I go through in detail in the upcoming part 3 of my CardRunners series on multi-street theory.
Computational Solution
Of course GTORangeBuilder can just solve this brainteaser numerically for us. I will go through a pencil and paper solution as well to illustrate the concepts and mathematics required to solve these types of problems, but since the pencil and paper solution is reasonably complex I'll give a solution summary and a browseable GTORB solution before I get into the nitty gritty of the analytic solution.
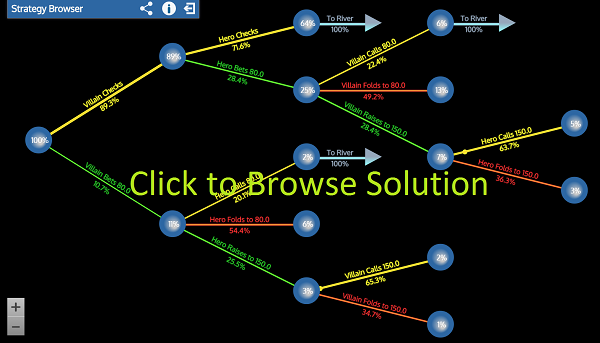
I'm only going to provide an analytic solution of the game where we do not pay the villain $3 to check so that we can see that it is actually optimal for him to lead for $50 against us. Calculating GTO strategies for the variations of the game (where our opponent is forced to check) can be done using the exact same techniques.
Solution Summary
- It is +EV to pay your opponent $3 to check, optimal play for the villain is to always lead the turn for half pot and this significantly increases his EV
- This game is more than double the EV for the villain than the game where the hero's range is half nuts, half air, even though his turn equity is only a few % higher.
- The hero's EV is higher here when he holds 1/3rd straight draws and 1/3rd flush draws than when he holds 2/3rds flush draws and no straight draws, even though flush draws are stronger hands.
- It is optimal for us to jam our strongest draws some of the time and call the rest. 150 chips is the exact break-even point where calling and folding a flush draw are equal EV, if stacks are any deeper it is +EV to shove/call a flush draw and we should mix between the two.
At first, the idea that the villain should bet his merged range into his opponents polarized range might be quite surprising. The reason for this is that while the villain is facing a somewhat polarized range on the turn, he is facing an even more polarized range on the river and by leading the turn he takes control of the pot size, rather than letting his opponent build the pot with a perfectly balanced range. It turns out that even if the villain were the check the turn, check jamming is higher EV than check calling.
In general, it often is GTO to get all the money in on the turn in situations where the river will put you at such an informational disadvantage that you won't be able to realize your equity.
The basic issue for the villain is that his informational disadvantage greatly increases on the river. This is due to the fact that on the turn the hero's straight draws and flush draws and roughly equivalent hands, so the informational advantage that the hero has by knowing his own hand, rather than just his range is minor, whereas on flush or straight runouts, these two hands become polarized, greatly increasing the value of knowing which specific hand of the two the hero holds.
Mathematical Solution
In this case what we will do is start by considering each of the OOP villain players 3 options for his first action and assessing their EVs when both players play GTO from that point forward.
The villains simplest option is to shove. In this case optimal play for the hero is to call with the nuts and fold the rest of his range.
Since the hero has the nuts 1/3rd of the time and the villains equity vs the nuts is 0, from the villains perspective the EV of this option is 1/3 * -150 + 2/3 * 100 = 50/3.
Next lets consider what happens if the villain bets $50. The hero can react by calling, folding or shoving? How can he optimally split his range between these three options? Lets start by examining what the hero should do with the nuts as that drives the rest of the strategy.
Clearly folding the nuts is a bad plan so the question is, is our EV higher with a shove or with a call?
Against a shove, the villain must call enough to make us indifferent between shoving and the highest EV of calling or folding of our potential bluffs.
Since a flush draw simply has more outs than a straight draw, it should be the higher EV hand both as a shove and as a call and thus we can conclude the villain must call a shove such that we are indifferent between jamming our FD and calling it or folding it (whichever of those two is higher EV).
At this point we're going to guess that jamming the nuts is optimal, which is easily checked as a final step. Intuitively jamming the nuts seems like a good guess as intuitively villain should have to call a turn jam more than a river $100 bet, as our bluffs have equity on the turn so we can jam more air.
So given that we are jamming the nuts, over a $50 lead we just need to figure out how to optimally allocate or flush and straight draws between calling, folding and jamming.
Lets consider what kind of range of range it might make sense to call with. First intuitive we can note that if we are calling with some flush draws, we should always call with some straight draws also. Why?
Suppose we call with x% of our flush draws. If we then call with y% of our straight draws and y = x/3 we can jam our entire range whenever a flush completes and our opponent's EV will be 0 because he will be calling 100 to win 300 so we want 1 bluff for every 3 value bets. As long as our range doesn't have too high a frequnecy of straight draws, our straight draw effectively whenever a flush or a straight completes because we can bluff shove them whenever the flush completes.
Similarly, by having both flush draws and straight draws in our calling range we can bluff some of our flush draws whenever a straight completes, further increasing our EV. Having both of these diverse draws that hit on different runouts increases our EV with both drawing hands by ensuring that our range nicely polarized on a variety of river cards, they have a lot of synergy.
So what are the optimal relative frequencies for calling with our flush draws and straight draws? If y > x/3, we are no longer able to usefully turn our straight draws into bluffs so their value goes way down. Optimal play requires that y = x/3 exactly.
What is the EV of calling a river bet with a range where y = x/3, that is it is exactly 3/4 flush draws and 1/4 straight draws?
Given our opponents hand there are 46 possible river cards.
7 complete our flush
6 complete our straight
2 complete both
31 are blank
Of those 31 blanks, our range blocks 2 of them 3/4 of the time and 2 of them 1/4th of the time, and 27 of them never, so effectively given the blockers from our range, there are 27 + 2 * 1/4 + 2 * 3/4 = 29 blanks
When our flush completes or both draws complete, our EV is the entire pot (minus the $50 we contributed to it) since we will bet and our opponent will just fold, so 150.
When the straight completes, we will bet our straights draws plus enough of our missed flush draws to make our nuts to air ratio 3 to 1, which means we will bet 1/3rd of the time and our ev will be the pot. So our EV in this case is 200 * 1/3 - 50.
When a blank comes our EV is just -50 since we always have to check fold.
As it turns out
(9 * 150 + 6 * (200 * 1/3 - 50) + 29 * -50) / 44 = 0
Calling with a balanced range of draws is exactly EV 0, which means we will be indifferent between calling, folding and shoving. Note that this is specifically due to the stack sizes. If the effective stacks were $151, the EV of calling with this range would be greater than 0 and we would never want to fold a flush draw, and if stacks were $149 we'd never want to call with a flush draw.
Furthermore, if we look at the hand specific EVs, they are both 0. With a flush draw, we hit our draw more often, but we can't bluff it as effectively when it misses and the other draw completes. Of course as soon as stacks get any deeper our EV for calling with a flush draw will become positive.
Now that we know the EV of calling with a FD and a straight draw is 0 so long as y = x/3, we can note that shoving a flush draw is always going to be better than shoving a straight draw, due to the slightly higher equity when called.
We should shove our flush draws such that our opponents EV for calling against our range of nuts + flush draws is equal to the EV of folding, -50. Call f how often we shove a flush draw, which has equity e when called. In this case e = 0.205
EV[call shove] = -150 * 1 / (1 + f) + f / ( 1 + f ) * (-150 * e + 250 * (1-e))
EV[fold to shove] = -50
These are equal when f = 0.4587. (wolfram alpha)
Now in this special case where the stacks are exactly $150 what we do with the rest of our range doesn't effect our EV. However, note that we assumed shoving the nuts was our highest EV option. Were we to try something else (say calling) with the nuts, we'd want to have enough bluffs on the river to maxmize our EV with the nuts, so I will consider the case where we call with all of the flush draws that we don't shove, although as we will see the strategies that folds some or all of the flush draws that aren't shoved are all also GTO.
It is easy to now directly calculate the EV of calling with the nuts and it turns out that it is significantly lower than the EV of jamming, I won't show that calculation here so as to keep this post short(ish).
Now that we've worked out the GTO response to a villain lead of 50 chips, we need to actually determine the EV of leading for the villain. Because the hero EV when he calls and folds is 0, and the villains EV when the hero shoves is -50, the EV is just
-50 * ((1+ f) / 3) + 100 ((2 - f)/3) = 27.08.
Computing the EV of checking for the villain can be done in the exact same fashion, but as we can see from the GTORB solution it is much lower EV for the villain to check.
I encourage you guys to experiment with the mathematical techniques above and to work out the checking EV on your own, but as it turns out leading is optimal for the villain and thus his EV in this game is 27.08.