Epsilon Equilibrium: How You Can Separate GTO Fact from Fiction

It turns out that any reasonably motivated player, armed with CREV can measure how close to GTO a strategy is, even in spots where actual GTO play is not known by employing a game theory concept called an Epsilon Equilibrium.  Epsilon equilibrium let us measure exactly how near to GTO strategies are and is a standard game theoretic technique that is used to compare the quality of various strategies.

See my latest videos below to learn more about how to compute epsilon equilibrium and why they are important.  This will also be a major topic in my upcoming Cardrunners video on Multistreet Theory and Practice.

Improving your turn play with GTO -- Check raising vs leading on the turn

As GTO strategy and computational GTO solutions have begun to take over mid/high stakes poker strategy more and more players are studying and analyzing GTO strategies in an attempt to improve their play.  However, many players find it difficult to bridge the gap between viewing and analyzing a specific GTO strategy solution to actually understanding how to use GTO analysis to directly improve their game play and I've gotten a number of requests for a more practical post that directly show how to use computational GTO solutions to improve your play at the tables.

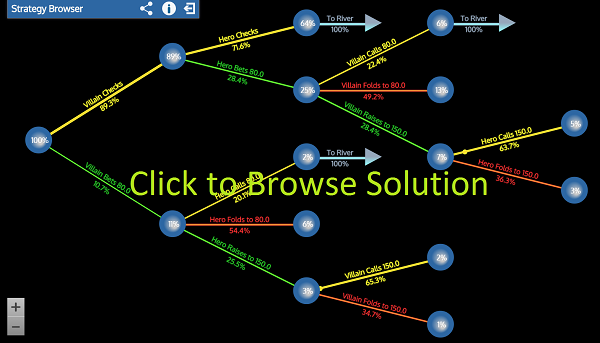
Today I'm going to give a simple example of how to use GTO poker and GTORangeBuilder to directly improve your play in a common real world situation that many players struggle with and show the general analytic process that I use in my strategy packs.  For the actual analysis I decided a video demo would be the most instructive, see below.  You can browse the solution that is discussed in the video here:

however before getting into the video I always wanted to take a second to answer three common questions that I often get from people who are new to computational GTO analysis.

1. Why should I study GTO, doesn't GTO play just break even against fishy players?  Don't I need to focus on exploiting the fish I play against?
• GTO play most definitely does not break even against fishy players, in general it crushes them.  The idea that GTO is a purely defensive or "break even" strategy is a misconception that comes from people often learning about it in very simple "toy game" situations like rock paper scissors or the clairvoyance game.  In real world poker situations GTO play extracts significant EV from both regs and fish, see here and here for more details.   GTO theory also lets us target specific leaks using a concept called minimally exploitative play and GTORB lets you lock in specific opponent strategies that you wish to minimally exploit.
2. Isn't GTO play just about understanding 1-alpha bluffing and calling frequencies?  Why do I need computational solutions?
• Before true computational GTO solvers like GTORB emerged, many players tried to "estimate" GTO play using the 1-alpha value derived from the clairvoyance game in the mathematics of poker which assumes one player has a purely nuts or air range and the other player can only possibly hold bluff catchers.  It turns out that once we had software that would let us actually calculate true GTO play in specific situations it become clear that these estimations were far from correct and missed many of the key strategic intricacies that exist in poker.  In the flop c-bet defense strategy pack I showed that defending vs flop c-bets at a 1-alpha frequency is usually a major mistake and in my Cardrunner's series I show that even in very simple river situations some of the best 1-alpha based ranges like those from Matt Janda's books are many times less accurate than computational solutions and can misplay key hands. 
3. GTO strategies are so complex that I could never hope to correctly play them at the tables, how can I actually learn anything that is useful to my everyday play from GTO solutions
• As I show in the video below, the goal of studying GTO play is not to try and directly copy the exact frequencies in your own play at the tables, but it is instead to gain a deeper understanding of the fundamental elements of strong poker strategy in specific types of situations.  In the video below I demonstrate how you can scientifically and precisely measure the EV importance of strategic options like donk-betting the turn, using different bet-sizings, etc to gain a deep understanding of the a complex real world poker situation.

GTO is so much more than unexploitable

One of the most common misconceptions that people tend to have regarding GTO poker play comes from the idea that somehow the key element of a GTO strategy is its "unexploitability" or "balance" and the belief that any unexploitable strategy is inherently GTO.

The conditions required for a strategy to be GTO are much stronger than simple unexploitability (although of course any GTO strategy must be unexploitable), and in a practical sense, the elements of GTO play that are generally going to be the most valuable to try and use in real world poker games are the elements that have nothing to do with unexploitability.  By focusing on unexploitability people minimize and miss what is actually the a huge part of the value of understanding GTO play.

Today I'm going to take a look at why people have come to often confuse the idea of unexploitability with GTO and go through the core definitions and a simple example that illustrates the key difference between a GTO strategy and one that is only unexploitable.  This will also serve as a nice lead in to my next post which will present a practical example of how to analyze and improve your 6-max OOP turn play in raised pots by better understanding GTO.

Toy Games and GTO

GTO play often gets confused with unexploitable play due to the fact that in the very simplest toy games the two are equivalent.  People learn the solution to the toy games, without fully understanding the definition of GTO and assume that they now know what GTO means.

Games like Rock Paper Scissors, or the Clairvoyance game from the mathematics of poker only have a single "reasonable" unexploitable strategy, which happens to also be fully GTO, which means that people who are new to game theory are prone to mistakenly assume that GTO and unexplotable are equivalent.

Furthermore, in these toy games, you can solve for that GTO solution using only indifference conditions (which only can be used to identify unexploitability) and thus the mechanism for finding the solution reinforces the idea that unexploitability is all there is to GTO.  In fact, most arguments I've heard against GTO play stem almost entirely from generalizing from the Clairvoyance game to all of poker without any thought to the idea that a game that is trillions of times bigger might be fundamentally different.

This happens because when solving toy games we usually automatically discard strategies that might be unexploitable but intuitively are obviously dumb.  However, this completely breaks down in extremely tough games because the "obviously dumb" decisions are no longer at all obvious, and in fact identifying and avoiding these "obviously dumb" leaks in large games is where a huge amount of the value of studying GTO play comes from.

Definitions

Lets go back to the core definition of a GTO strategy, which is a strategy for a player that is part of a nash equilibrium strategy set.  In a 2 player game a strategy pair is a nash equilibrium if, "if no player can do better by unilaterally changing his or her strategy" (source wikipedia).

How does this actually tie into the concept of exploitability and in a technical sense, what does exploitability actually mean?  The idea of exploitability is relatively intuitive, if your strategy is exploitable, it means that if your opponent know your strategy they would be able to use that information to alter their own strategy in a way that would increase their EV against you.  Formalizing the above, gives us an accurate definition of exploitability, but we need to define one more concept first.

A "best response" (sometimes called a "maximally exploitative strategy", or "counter strategy") to a given opponent strategy is a strategy that maximizes our EV against that opponent strategy, assume that his strategy is completely fixed.

Exploitability can now be defined (and measured) as follows.  Call G our GTO strategy, and S our opponents strategy.  Call B the best response to S.  S is exploitable if our EV when we play B against S is higher than our EV when we play G against S and that EV difference is the magnitude of the exploitability.

Intuitively, this should make perfect sense, our opponents strategy is only exploitable if we can alter our own strategy to exploit him and increase our EV, and the amount of EV we can gain when we maximally exploit him is an accurate measure of the magnitude of his exploitability.

Any GTO strategy must be unexploitable to satisfy the definition of a nash equilibrium, but in complex games there are usually infinitely many inferior unexploitable strategies that are not GTO.

A GTO strategy, is a strategy that is using every possible strategic option and every synergistic interaction between various hands in our range to maximize our EV while also still being unexploitable.  In most real world cases, understanding which of our strategic options are strong and how to correctly leverage that strength against our opponent in ways they cannot prevent is what makes GTO play powerful.

An Example -- GTO Brainteaser #6

Armed with our definitions we can now look at a very simple example of a unexploitable, non-GTO strategy.  Keep in mind that even this example is a relatively simple toy game and that the real game of poker generally has infinitely many unexploitable strategies that pass up EV and are not GTO for far more complex reasons.

We're going to revisit the model game from GTO Brainteaser #6.  The setup is as follows:

There are 2 players on the turn with 150 chip effective stacks, and the pot has 100 chips.  The Hero has a range that contains 50% nuts and 50% air and he is out of position.  The Villain has a range that contains 100% medium strength hands that beat the Hero's air hands and lose to his nut hands.

For simplicity, assume that the river card will never improve either players hand.

The hero has 2 options, he can shove the turn or he can bet 50 chips.  If the hero bets 50 chips on the turn he can then follow up on the river with a 100 chip shove.

As I show here it turns out that GTO play for the hero is to bet 50 chips on the turn and then 100 chips on the river with precisely constructed ranges that contain the right relative frequency of nuts and air, and to check/fold with the rest of his air.  Following this strategy gives the villain an EV of 11.11 chips.

GTO play for the villain is to call a 50 chip turn bet or a 100 chip river bet 2/3rds of the time and to call a turn shove 40% of the time.

Now consider the non-optimal strategy S where the hero shoves the turn 100% of the time with the nuts and 60% of the time with his air, and check/fold sthe rest of his air.  It is easy to check that the EV of this strategy is 20 chips for the villain.  So we are giving our opponent almost double the EV by playing this weaker strategy S where we jam the turn.

Clearly S is not GTO, we could unilaterally increase our EV by switching to the GTO strategy, because S is fundamentally not wielding our range and our stack to optimally prevent our opponent from realizing his equity.

However, S is completely unexploitable.  Because our turn shoving range is "balanced" to be 3/8ths bluffs our opponent is exactly indifferent between calling and folding to a shove so he cannot increase his EV by switching from his GTO strategy to a maximally exploitative strategy.

Someone looking for an "unexploitable" strategy might be happy with the strategy S, but in this case, S misses the entire practically valuable lesson that we can learn from the model, which is that by betting half pot twice we actually utilize our polarized range much more effectively than we do by shoving it, to the extent that we cut our opponents EV approximately in half.  The entire point of the example and its power is completely lost if we focus on unexploitability rather than on EV maximization and the true definition of GTO.

In fact our EV if we play an exploitable strategy where we bet 50 chips and then jam the river for 100, but with slightly incorrect value bet to bluff ratios is much higher than it is when we play the unexploitable strategy S, even if our opponent perfectly exploits us.

Similarly, when analyzing complex real world situations, focusing on unexploitable play is generally going to completely miss out on valuable lessons that a thorough study of GTO play has to offer.

Special thanks

This post was actually largely inspired by an email from a GTORangeBuilder user who was confused that using CardRunners EV's "unexploitable shove" option didn't give him a GTO strategy like GTORangeBuilder does.  Of course the feature does exactly what it says, it gives a range that is the best range for us to shove if our opponent perfectly counters our shove, which in no way suggests that the shoving range is actually GTO.

GTO Brainteaser #9 -- Multistreet Theory: Range Building with Draws

This week we are going to examine a multi-street game, starting from the turn where one players range consists of the nuts and draws while his opponents range consists of a medium strength hand that never improves to the nuts.   I'll be going over this game in depth and providing a solution in part of my next CardRunners video which should come out in a few weeks.

Not that this is almost identical to the game that we examined in GTO Brainteaser #6 except that in this case, the hero's turn bluffs have the potential to improve on the river.  In both games the player with the merged range has about 50% equity (in this game he has 53.8%).

The setup is as follows:

1. There is a $100 pot, and we are on the turn with $150 effective stacks.  
2. The board is AsTs9c2d
3. The hero is in position and his range is 1/3 nuts, 1/3 straight draws and 1/3rd flush draws, specifically, the hero holds either 7s3s, 8h7h, AcAd.
4. The villains always holds a medium strength hand, KcKd
5. Both players are allowed to either check, bet 50% pot, or shove on both the turn and the river.
6. Your opponent plays GTO

The villain offers to always check the turn to you if you pay him $3 should you accept his offer?  What does GTO play look like in this game for both players?  Is this game higher EV or lower EV for the villain than the nuts/air game from GTO Brainteaser #6?

Would the hero be better or worse off if his range was 1/3 nuts 2/3 flush draws?  How would optimal play change?

GTORB Turn Launched -- Multistreet theory video coming soon

The latest version of GTORB can now solve turn scenarios and is available for purchase!  For a sneak peak of what a solution looks like see this post.

I've been putting most of my time towards the turn solving code lately so I haven't had time to do as much blogging / video creation, but now that the turn solver is released I'll be releasing a series of blog posts as well as a CardRunner's video on multistreet GTO theory with example turn solutions over the coming month, stay tuned!